I guess it depends on what you mean by
one step. The Hack ALU certainly requires only one Hack machine
instruction to negate a number supplied as input to the ALU. There are actually 2 versions of an instruction that that does this - to arithmetically negate either the x-input or the y-input of the ALU.
I guess you could think of "steps" in terms of the individual logical elements required to actually execute the instruction as identified in the ALU specification provided in Figure 2.5b (2nd edition of the book). This is shown for educational purposes in the annotated snip below.
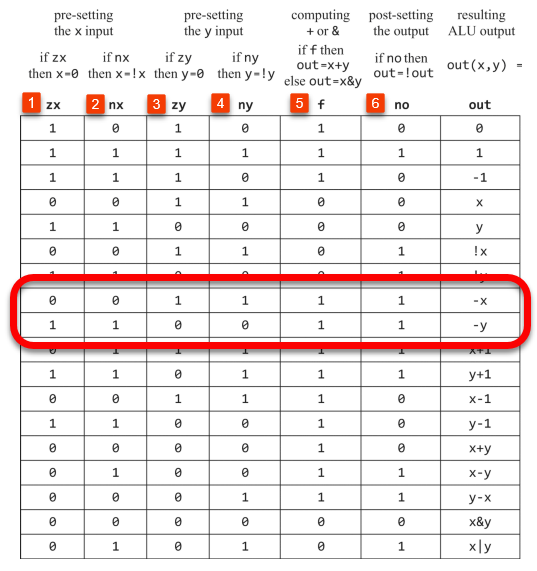
For example, there are six actions that must happen to produce the negative of a value provided to the x-input of the ALU. You might consider these "steps", although the authors don't refer to them in that way. As far as I can tell, the term "steps" is undefined in the context of the Hack computer. If this is the sense in which HighSchoolerWhoAsksHowTooMuch means "steps", then his statement about the number of steps the Hack ALU requires to negate a number seems correct. By the same token then, a "step" and an "instruction" must now mean entirely different things.
WBahn is absolutely correct in saying that only one i
nstruction is required to negate a number because all the logic to do so is completely executed in a single clock cycle. His algebraic description of how the negation is produced kind of describes these "steps". The ALU, in "Step 5", adds -1 (produced at y-input by "steps" 3 and 4) to the number to be negated at the x-input (unchanged by "steps" 1 and 2), then "flips" the bits of that sum ("step" 6) to create the ALU output for the instruction. All this happens in a single clock cycle in the Hack ALU. The original confusion, I think, results from the way the ALU does negation. It's conceptually different from the way the authors describe how to do it in their discussion of 2's complement arithmetic. As WBahn has pointed out, the same result is produced either way.