Inspired by
Mark's 440-NAND ALU, I came up with a 403-NAND implementation of my own. It uses 21 NANDs per bit for the operation (minus 3 because we don't need the last carry bit), 46 NANDs for the zr bit, and 24 NANDs for preprocessing of the control bits.
How this works:
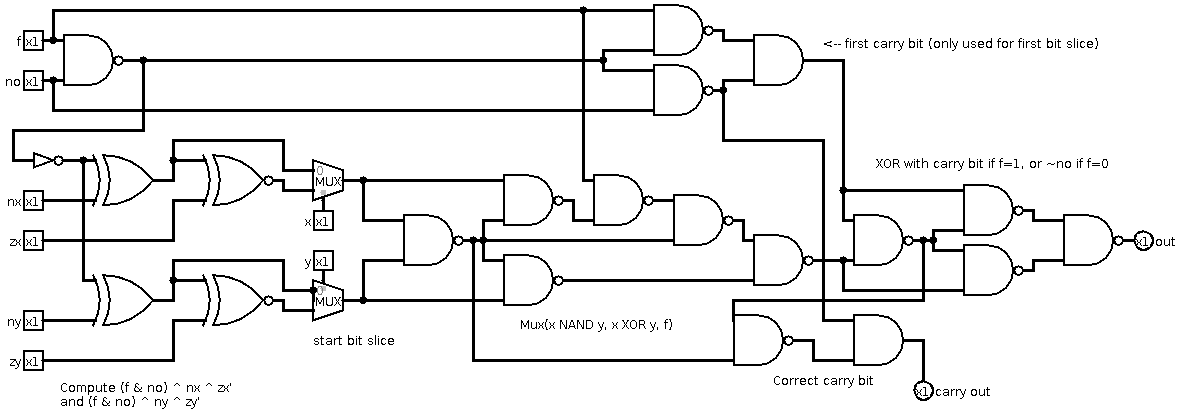
Following the specification literally, we first want to compute (x & ~zx) ^ nx and (y & ~zy) ^ ny, then run them through the adder, then mux the NAND and the sum with f, then XOR with no. Mark's main innovation was to compute (x & ~zx) ^ nx as Mux(nx, nx ^ ~zx, x), saving three NANDs per bit (npb) on the naive implementation. By also cleverly avoiding a bitwise negation of x NAND y, Mark saves 3 + 3 + 1 = 7 npb, at an additional constant cost of 15 gates. My new implementation is based on the following observations:
1) In two's complement arithmetic, ~(x+y) = ~x + ~y + 1, so we can negate an addition by negating the inputs and adding 1. Adding 1 is easily implemented by using a full adder for bit 0 and setting the carry bit to 1.
2) Define B(x,y,f) = Mux(x NAND y, x XOR y, f). x NAND y is already computed by the first XOR in a full adder, so by changing the first XOR to B(x,y,f) and setting the carry bit to ~no if f = 0, the output of the second XOR will equal the output of the ALU. It is possible to implement B(x,y,f) in 6 npb, simultaneously computing x NAND y so that it can be used for the carry bit in an addition operation.
3) Similarly to a full adder, the outgoing carry bit is computed with (x NAND y) NAND (B(x,y,f) NAND c), where c is the incoming carry bit. If f = 1, nothing changes from the usual adder. However, if f = 0, then B(x,y,f) = x NAND y, so the outgoing carry bit becomes x & y if c = 0, and 1 if c = 1. When f = 0, we want all of the carry bits to be equal to ~no, so if no = 0 and we set the first carry bit to 1, then this carry bit will propagate through the remaining bit slices, giving correct behavior. It therefore remains to correct the behavior when f = 0 and no = 1. This can be done in two npb with c & (no -> f), which is equal to 0 when f = 0 and no = 1, and equal to c otherwise.
In summary, my implementation eliminates the final XOR for negating the output and simplifies the AND/ADD mux, at the cost of additional complexity for handling the carry bit. In total, I save 4 + 1 - 2 = 3 npb, at a net constant cost of 11 gates, for a total of 403 gates.
Here's a picture of the circuitry for preprocessing the control bits and handling the first bit of the operation: