Printing Pi to 20ish d.p.

[Lozminda]

With this post in mind:

http://nand2tetris-questions-and-answers-forum.32033.n3.nabble.com/Experienced-People-Please-share-your-struggles-tt4034156.html#a4034226

And following on from my post 2 March 2020 on the Mandelbrot Set, I present Pi to  20 ish d.p using the same class that I used to generate the Mbrt Set. Well until it crashed I guess (59!)/(61!!) was a bit too large. My bad, the class can handle that kind of number, but I don't have enough time atm to fettle that much..

Here are some screen shots




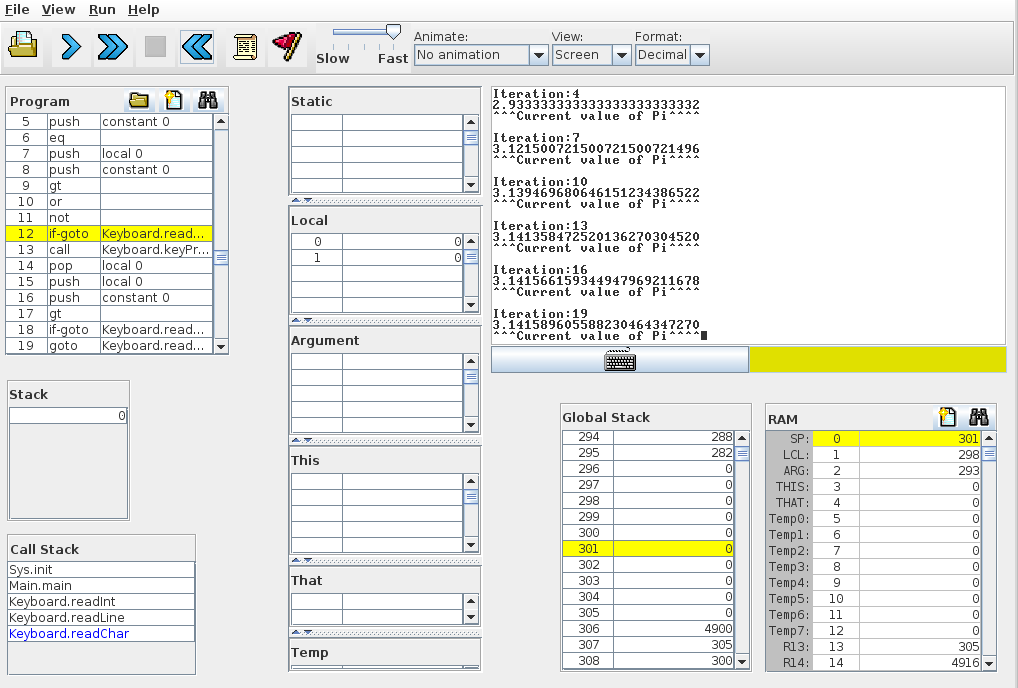
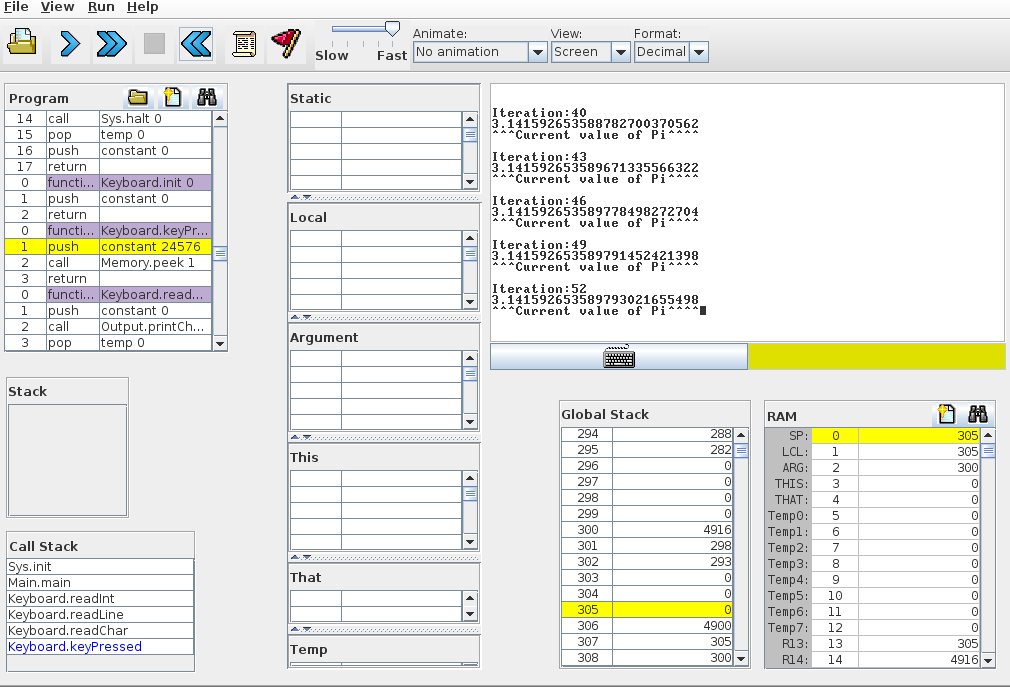
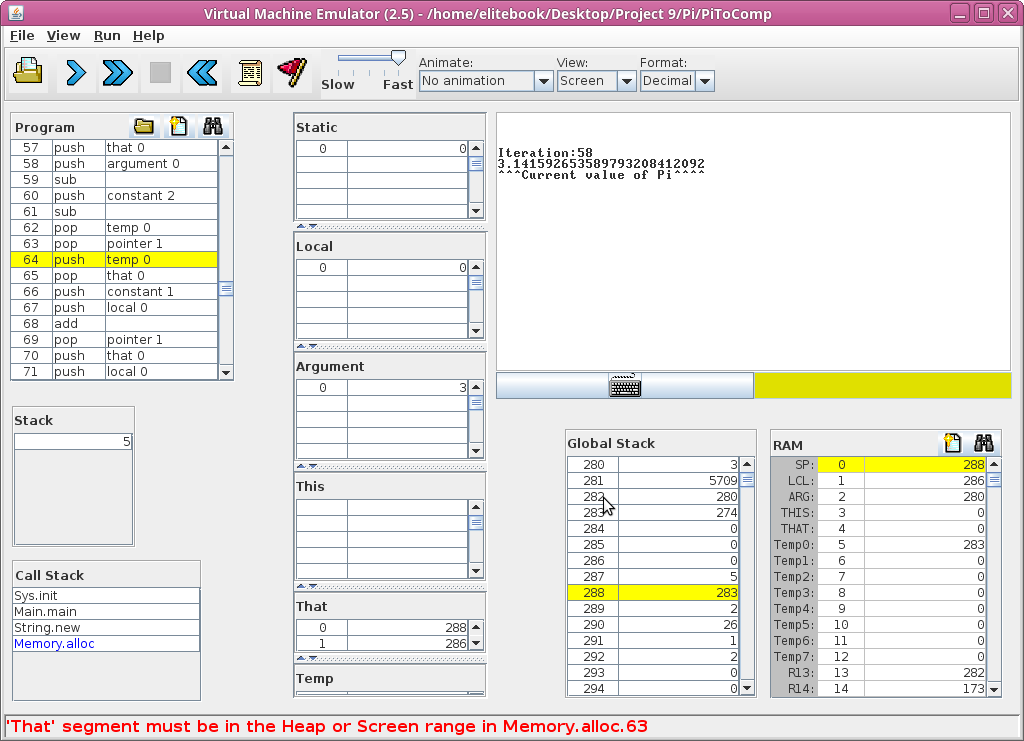
And the code (sorry there's absolutely no comments, but if you check out the formula in the Please-Share-your-sruggles post) it should be fairly self explanatory, I hope)  




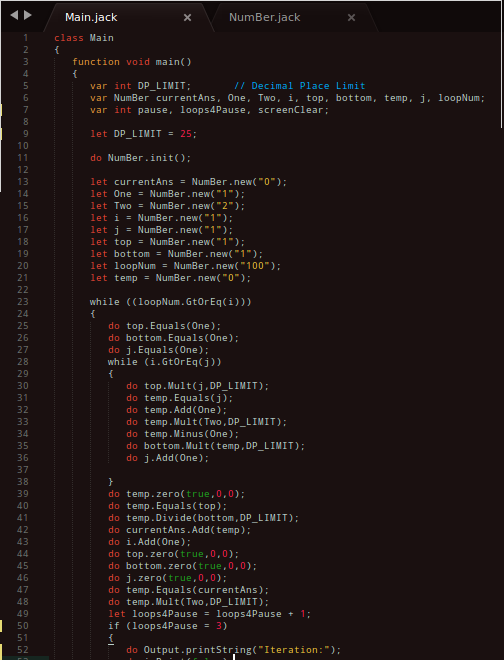
It's a slightly older version than the class I used to generate the Mandelbrot set, hopefully once my work life has sorted itself out, I might be able to do something important and get back to N2T and post some more Mbrt stuff.

Code On !

Lozminda

[ivant]

This is great! I think you should publish your code (at least the NumBer class) on github or similar place. It looks quite useful.

[WBahn]

Lozminda wrote

And following on from my post 2 March 2020 on the Mandelbrot Set, I present Pi to  20 ish d.p using the same class that I used to generate the Mbrt Set. Well until it crashed I guess (59!)/(61!!) was a bit too large. My bad, the class can handle that kind of number, but I don't have enough time atm to fettle that much..

Assuming that that is (59!)/(61!), this it is really only 1/(60*61). I would imagine a pretty simple tweak to your algorithm should be able to exploit that.

[Lozminda]

Hi ivant

You've noticed that I haven't published the code for NumBer and there's a good reason for that. I will do eventually (barring death or serious injury) how ever N2T isn't the only thing I'm working on (the jack program is a proof of concept if you like) and I'd like to publish some other things in more "useful" languages first, before N2T.  (Having done the work I'd like to be the first to publish, does that make me some kind of ego maniac ? Possibly ?)

Work (which isn't coding) is still being exceedingly time consuming atm, which isn't helping anything except finance possibly.

All will be eventually revealed, but that's possibly going to be in a year or so (hopefully less) (I could give up N2T, work on the other stuff and then come back to N2T, but I've already had quite a break doing this). Sorry to be slightly cloak and dagger, but there's nothing worse than working really hard and then someone else taking all the credit ! (Well there are lots of worse things, but you know what I mean..)

Again thanks for your comments, nice to have that little bit of extra motivation.

Lozminda

[Lozminda]

Dear WBahn,

Don't forget it's 59!/61! !

I'll just have a check for simplification, I'm sure you're right, but the reason for using the formula as is (and there are many, as I'm sure you're aware, more efficient formulas for deriving Pi) is to test the class NumBer.
I.e. I want it to be successful at handling big numbers and doing tricky operations with them i.e. divide, as this program is a simple testing environment for that. The value of Pi having previously calculated to zillions of d.p. so one has an easy check at the end. Each operation has to be completed successfully too, to get the right result.

I'll have a quick look at the simplification now...

Cheers

[Lozminda]

Re simplification

Just to keep it reasonably simple I'm gonna look at the 7th term.
(N.B. ---------- should be a solid line i.e. it represents divide)

    1.2.3.4.5.6.7
----------------------
1.3.5.7.9.11.13.15

=>

    2.4.6
--------------
9.11.13.15

if I haven't made any mistakes you're absolutely right (not that I had any doubts), but would it be easier to code ?
You've got:

               (n-1)!!
----------------------------------------
not sure what this term should be

Great to see someone taking an interest, thank you !

Lozminda

[WBahn]

Lozminda wrote

Dear WBahn,

Don't forget it's 59!/61! !

I can't forget it since I haven't been told it. By this I mean that, as near as I can tell, you haven't given the basic equation you are using to calculate pi -- and there are many of them.

But I'm not aware of ANY that would use a factorial of a factorial.

To show how insanely fast this grows, while 47! requires less than 200 bits to represent, 47!! has more bits than there are atoms in the known universe.

[WBahn]

In doing some searching I think I see what you are using (perhaps), but more to the point what the !! operator probably means.

I found the Newton/Euler convergence formula expressed as

pi/2 = SUM{n=0 to oo) n! / (2n+1)!!

with the note that k!! is the product of the odd integers up to k (and where k is odd).

I've never seen this notation before and I think it is horrible as it redefines a perfectly valid and well defined operation. This would be like saying that --x isn't -(-x) = x, but rather that --x denotes x^pi or some other locally useful meaning.

While I'll admit that using this notation makes the equation "prettier", it is not needed. It's easy to express

(2n+1)!! = (2n+1)! / [(2^n)(n!)]

Which makes

pi/2 = SUM{n=0 to oo) (2^n) (n!)^2 / (2n+1)!

This is an expansion that looks pretty useful (I don't know if it helps you are not).

pi/2 = 1 + (1/3)(1 + (2/5)(1 + (3/7)(1 + .... (n/(2n+1))))

[Lozminda]

In my defence, the formula I'm using is in my OP in the form of a link to another post, which should take one to the formula I'm using.

Apologies if not, it does when I tested the link in my browser.