1.1.1 text elaboration request

[linuxford]

First, thank you for this excellent and very unique book. Amazing!

Questions on "Canonical representation" and "Two-input boolean function."

Let me try to be a bit more precise. 1. Canonical representation - I got the fact that and-ing bears uncanny resemblance to multiplication and or-ing to addition. Curious about the picking function formulation of f(xyz) = ~xy~z + x~y~z + xy~z. I understand how you determined to pick the formula but curious why this works.
2. Two-input boolean function - I'm wondering why it works out to be 2^2^n

Thanks again for any feedback.

[cadet1620]

linuxford wrote

Let me try to be a bit more precise. 1. Canonical representation - I got the fact that and-ing bears uncanny resemblance to multiplication and or-ing to addition. Curious about the picking function formulation of f(xyz) = ~xy~z + x~y~z + xy~z. I understand how you determined to pick the formula but curious why this works.

2. Two-input boolean function - I'm wondering why it works out to be 2^2^n

1. The first row in figure 1.1 that has a 1 as its output requires that x=0, y=1, z=0. If x=0 then ~x=1. So for this row in the truth table ~x=1, y=1, ~z=1, so anding them together results in 1. ~x y ~z will only be 1 for this combination of inputs.

The other two and terms work similarly.

These terms that generate 1 for the required rows are ored together so that the function will output 1 if and only if one of the row selecting and terms has detected its correct combination of inputs.

2. For n input variables, the truth table will have 2ⁿ rows. Since there are two choices for the output value for each of these 2ⁿ rows, the number of combinations is 2⁽²ⁿ⁾.

--Mark

[linuxford]

I had a suspicion about #1 and you confirmed what I figured after a couple of hours thinking about it. But it was great to hear your explanation and shore up my suspicion.

The #2, I didn't get the connection until I read your reply. I can now see that I needed to apply the Canonical rule to the table in Figure 1.2

Great I think I got it. Thanks a lot.

This book is amazing, I've seen a lot of texts over the 20 years in the semiconductor business, and this book is an absolute unique gem that I've never seen and I've browsed hundreds of books and many hours in bookstores. I was fortunate to recently stumble upon this book on Amazon.

[cadet1620]

linuxford wrote

The #2, I didn't get the connection until I read your reply. I can now see that I needed to apply the Canonical rule to the table in Figure 1.2

Figure 1.2 doesn't have anything to do with canonical form. Canonical form means the ANDs followed by OR implementation of a function. Figure 1.2 is simply a truth table with 16 outputs, turned sideways. (See figure 2.2 for an example of a 2-output truth table.)

--Mark

[linuxford]

Thank you for the reply :)

Let me restate what I am thinking after your feedback to see if I am understanding better.

So the formula 2^2^n "reveals the number of possible Boolean functions," which is in this case is 2^4 or sixteen different possible functions. On the right side of the table look to be the different bit pattern options or results that the function could take (0000, 0001 .. 1111).

Each of these patterns has an associated name "Constant 0, And .. Constant 1." I am wondering about the Boolean function next to the name, which are "0, xy .. 1." Are these generated from the Canonical AND-ORing?  Some of them look like that directly.

For instance the XOR.



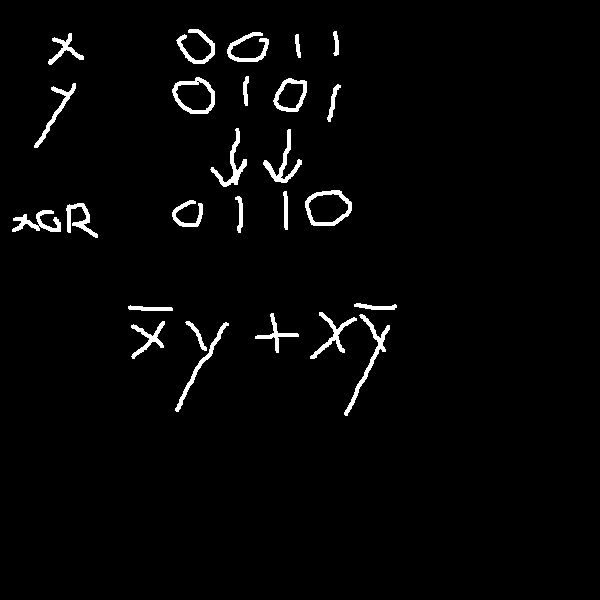
and others look like they "may be" some algebraic equivalent of some sort.

Thanks.

[cadet1620]

Except for AND, OR, NOT and ZERO you can implement the functions in canonical form, but it is often not the best implementation. The canonical form of TRUE would be:
    TRUE = xy + x~y + ~xy + ~x~y

Canonical form is just a tool that helps get you started. Consider that the canonical form of a 4-input function could need up to 15 4-input AND gates and a 15-input OR gate.

For most of this chapter, and the rest of the book, you will need to think about how to build more complex circuits using circuits you've already designed. HDL gives you Nand, true and false and you need to design
    Not using some combination of Nand, true and false,
    And using some combination of Not, Nand, true and false,
    Or using some combination of And, Not, Nand, true and false,
    etc.

--Mark

[linuxford]

I am looking at the truth tables of what I am trying to get to, and then the truth tables of the pieces and then play around with the pieces (gate implementation) until it outputs what I need. As I practice doing this more, it seems to get more intuitive. Sometimes the Canonical form is what I go with, for instance with the Mux.

This is making more sense to me, thanks a lot for your insights.