The expanded truth table for mux will have inputs sel and in and outputs a and b:
sel|in || a | b
---|---||---|---
0 | 0 || 0 | 0
0 | 1 || 1 | 0
1 | 0 || 0 | 0
1 | 1 || 0 | 1
Since there are two outputs, you need two Karnaugh maps, one for each output. Since there are only two variables, they are going to be 2 by 2 k-maps, which are not too interesting.
When you have more than 2 inputs, then things become more interesting. For the optimum solution you need to start by looking for minterms that are common to both k-maps.
Say we have a part with three inputs a, b, and c, and two outputs F and G whose k-maps are:
| bc | bc
F | 00 01 11 10 G | 00 01 11 10
---+---+---+---+---+ ---+---+---+---+---+
0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
a +---+---+---+---+ a +---+---+---+---+
1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
+---+---+---+---+ +---+---+---+---+
F and G have the minterm (~b)c in common so that Not and And gate can be shared with the circuits for both outputs.
F = ab + (~b)c
G = (~a)(~c) + (~b)c
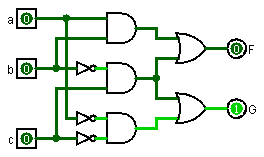
This can get complex rather quickly. Especially when you add "don't care" values to the functions.
--Mark