Mux and Boolean Algebra.

[Wnt2bsleepin]

I am trying to create a Mux, but I wanted to do so using a boolean algebra. I have the truth table for one

A|B|Sel|Out
0 0   0    0
0 1   0    0
1 0   0    1
1 1   0    1
0 0   1    0
0 1   1    1
1 0   1    0
1 1   1    1

I converted it into an expression
  ____        ___    _
ABSel + ABSel + ABSel

which I believe I simplified correctly using a K table.

SelB + SelA + AB

My question is, did I make any mistakes along the way? I am teaching myself, but I am afraid of getting the logic wrong at an early start. I am also unsure of how to convert this into logic gates. Thank you for any help.

[cadet1620]

[It works much better to write expressions using ~(x) since it's hard get the over-bars aligned across all browsers.]

The truth table gives the canonical expression
    (a)(~b)(~sel) + a(b)(~sel) + (~a)(b)(~sel) + (a)(b)(sel)
Putting these terms into a k-map gives
   
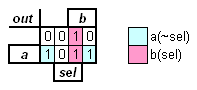
The minimum required terms are (a)(~sel) and (b)(sel).

A common mistake when learning k-maps is not to recognize terms that wrap around the edges as in (a)(~sel). Also note that in 4x4 k-maps, the 4 corners are a term.


An easy way to convert expressions to gates is to rewrite them in "function" form. For example
    (a)(b)(~c)+d
is
   OR (AND (AND (a,b), NOT (c)), d)

--Mark

[Wnt2bsleepin]

Ok, I was a little confused on what symbology to use.


The K-Map I got from the truth table looks a little different. I am not sure if they are the same though.

https://docs.google.com/spreadsheet/ccc?key=0AmeTrBG22eggdDdhTXpBOXhfQzVpM1JMRHJNVVluSVE&usp=sharing

(I don't know how to make a quick neat one)

Finding the groups of 1, I was able to figure out:

SelB + SelA + AB, but none of them are NOTs.

Just for clarification. AB is an AND and the + is an OR right?

I converted that into the wrong form of gates though

Or(And(Sel,B), Or(And(A,B),And(Sel,A)))


EDIT:

I made the google doc public. Sorry about that.

[cadet1620]

Wnt2bsleepin wrote

The K-Map I got from the truth table looks a little different. I am not sure if they are the same though.

https://docs.google.com/spreadsheet/ccc?key=0AmeTrBG22eggdDdhTXpBOXhfQzVpM1JMRHJNVVluSVE&usp=sharing

(I don't know how to make a quick neat one)

My k-map is a screen shot from Excel with light gray cell boundary lines erased with Paint.

Your k-map is the same as mine above, just with the variables in a different order. (I ordered mine specifically to show the split term.)

In your arrangement the k-map looks like this
   
The row/column labels indicate when a variable is true.

In a 3-variable k-map, rectangles of 2 ones are two-variable terms. There are 3 two-variable terms as highlighted above. To cover all the ones in the map, only two of the terms are required -- the red and blue ones -- so the minimized solution is those terms ored together.
    A ~Sel + B Sel

[I put () or spaces in for Ands so that there are visually two variables involved. My immediate read of SelA is a single signal named "SelA", which would be a selection signal for a part/bus named A.]

--Mark

[Wnt2bsleepin]

I actually got the same thing from my graph, except I didn't label Sel as 0. I also didn't exclude the AB combination. Why did you exclude the AB combination, and is there a common way to do this for all K Graphs?

[cadet1620]

Wnt2bsleepin wrote

I actually got the same thing from my graph, except I didn't label Sel as 0. I also didn't exclude the AB combination. Why did you exclude the AB combination, and is there a common way to do this for all K Graphs?

The point of a Karnaugh Map is to minimize the amount of logic required for the circuit.  Once you have the 1s placed in the map, find the smallest number of squares and rectangles that will cover all the 1s.

Take a look at http://www.facstaff.bucknell.edu/mastascu/elessonshtml/Logic/Logic3.html for a good introduction to Karnaugh Maps.

--Mark

[Wnt2bsleepin]

I got it for the Mux, thanks for the link as it was very helpful.

How would I do this for a problem that has 2 outputs like a DMux?

[cadet1620]

Wnt2bsleepin wrote

I got it for the Mux, thanks for the link as it was very helpful.

How would I do this for a problem that has 2 outputs like a DMux?

Each output is a separate equation, thus a separate k-map.  Make sure the input variables are in the same location on all the maps.  If you can find identical rectangles of 1s in more than one map, you have a term that can be used in both equations, saving a bit of hardware.

--Mark

[Wnt2bsleepin]

OK, I did the map for it. I got this based on this truth table

In Sel | A B
 0  0     0 0
 0  1     0 0
 1  0     1 0
 1  1     0 1

Top A, Bottom B





Should I essentially overlay them on top of each other to find the pairs? In this case, I got

SelIn + ~SelIn

[cadet1620]

The 1 in the A table is in the wrong place. It should be in the upper right position where IN is 1 and SEL is 0.

In this case, there are no 1s in the same locations so there is not commonality between the function for A and the function for B.

Here's an example where there is commonality.

The (~A)C term occurs in both functions X and Y.

X = (~A)C + A(B)(~C) + A(~C)(~D)
Y = (~A)C + (~A)B

--Mark

[Wnt2bsleepin]

Sorry, I reversed the Axis when I copied them from my paper. So, there are no groups at all, how do you come up with an equation for the components?

[cadet1620]

If there are no groups in common then you treat it as two unrelated maps.

--Mark

[Wnt2bsleepin]

So, if there are no groupings, then there is no simplification possible?

I don't understand how to connect the two and generate an equation.

[cadet1620]

For the DMux, you don't generate an equation. You need to generate two equations; one for the A output and one for the B output.

The truth table and the k-maps you made tell you that the A output is true when IN is true and SEL is false. The B output is true when IN is true and Sel is TRUE.

--Mark